Home / Publications / On the method of quasi-steady-state approximation

On the method of quasi-steady-state approximation

Nikolai Khristoforovich Petrov 1
Nikolai Khristoforovich Petrov
1 Photochemistry Center, FSRC ‘Crystallography and Photonics’, Russian Academy of Sciences, Moscow, Russian Federation
10.1016/j.mencom.2023.01.032
Published 2022-12-26
Communication , Volume 33, Issue 1, 103-106
2
Share
Cite this
GOST
 | 
Cite this
GOST Copy
Petrov N. K. On the method of quasi-steady-state approximation // Mendeleev Communications. 2022. Vol. 33. No. 1. pp. 103-106.
GOST all authors (up to 50) Copy
Petrov N. K. On the method of quasi-steady-state approximation // Mendeleev Communications. 2022. Vol. 33. No. 1. pp. 103-106.
RIS
 | 
Cite this
RIS Copy
TY - JOUR
DO - 10.1016/j.mencom.2023.01.032
UR - https://mendcomm.colab.ws/publications/10.1016/j.mencom.2023.01.032
TI - On the method of quasi-steady-state approximation
T2 - Mendeleev Communications
AU - Petrov, Nikolai Khristoforovich
PY - 2022
DA - 2022/12/26
PB - Mendeleev Communications
SP - 103-106
IS - 1
VL - 33
ER -
BibTex
 | 
Cite this
BibTex (up to 50 authors) Copy
@article{2022_Petrov,
author = {Nikolai Khristoforovich Petrov},
title = {On the method of quasi-steady-state approximation},
journal = {Mendeleev Communications},
year = {2022},
volume = {33},
publisher = {Mendeleev Communications},
month = {Dec},
url = {https://mendcomm.colab.ws/publications/10.1016/j.mencom.2023.01.032},
number = {1},
pages = {103--106},
doi = {10.1016/j.mencom.2023.01.032}
}
MLA
Cite this
MLA Copy
Petrov, Nikolai Khristoforovich. “On the method of quasi-steady-state approximation.” Mendeleev Communications, vol. 33, no. 1, Dec. 2022, pp. 103-106. https://mendcomm.colab.ws/publications/10.1016/j.mencom.2023.01.032.
Views / Downloads
1 / 5

Keywords

Michaelis–Menten mechanism.
quasi-steady-state approximation
singular perturbation
small parameter
sufficient conditions

Abstract

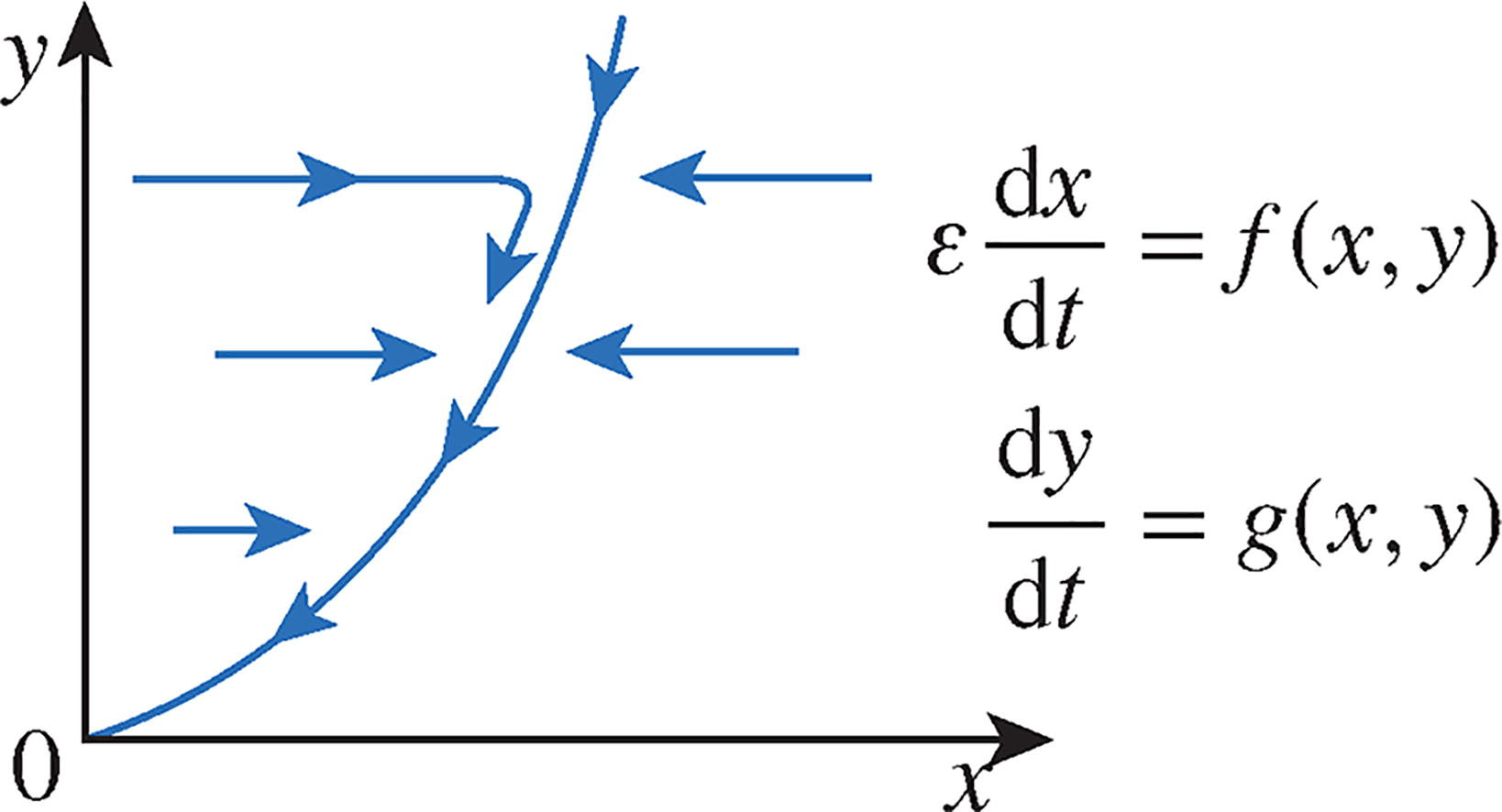
Sufficient conditions for the validity of the quasi-steady-state approximation widely used in chemical kinetics are considered by means of the qualitative geometric theory of differential equations with small parameters.

References

.
Kondratiev V.N., Nikitin E.E.
2011
.
The Induction Period in Chain Reactions
Benson S.W.
Journal of Chemical Physics, 1952
.
Eine Theorie der photochemischen Reaktionsgeschwindigkeiten
Bodenstein M.
Zeitschrift fur Physikalische Chemie, 1913
.
The steady-state approximation: Fact or fiction?
Farrow L.A., Edelson D.
International Journal of Chemical Kinetics, 1974
.
Tikhonov A.N., Vasil’eva A.B., Sveshnikov A.G.
1985